Snakes and Ladders, Estimation and Stats (or 'Sometimes It Takes Ages')
Snakes And Ladders
Simple kids game, roll a dice and move along a board. Up ladders, down snakes. Not much to it?
We’ve been playing snakes and ladders a bit (lot) as a family because my 5 year old loves it. Our board looks like this:

Some games on this board take a really long time. My son likes to play games till the end, so until all players have finished. It’s apparently really funny when everyone else has finished and I keep finding the snakes over and over. Sometimes one player finishes really quickly - they hit some good ladders, few or no snakes and they are done in no time.
This got me thinking. What’s the distribution of game lengths for snakes and ladders? How long should we expect a game to take? How long before we typically have a winner?
Fortunately for me, snakes and ladders is a very simple game to model with a bit of python code.
Firstly, here are the rules we play:
1) Each player rolls a normal 6 sided dice and moves their token that number of squares forward. 2) If a player lands on the head of a snake, they go down the snake 3) If a player lands on the bottom of a ladder, they go up to the top of the ladder. 4) If a player rolls a 6, they get another roll 5) On this board, some ladders and snakes interconnect - the bottom of a snake is the head of another, or the top of a ladder is also the head of a snake. When this happens, you do all of the actions in turn, so down both snakes or up the ladder, down the snake. 6) You don’t need an exact roll to finish, once you get 100 or more, you are done.
To model the board in python, all we really need are the coordinates of the snakes and the ladders - their starting and ending squares.
def get_snakes_and_ladders():
snakes = [
(96,27),
(88,66),
(89,46),
(79,44),
(76,19),
(74,52),
(57,3),
(60,39),
(52,17),
(50,7),
(32,15),
(30,9)
]
ladders = [
(6,28),
(10,12),
(18,37),
(40,42),
(49,67),
(55,92),
(63,76),
(61,81),
(86,94)
]
return snakes + laddersSince snakes and ladders are both mappings from one point to another, we can combine them in one array as above.
The game is moddeled with a few lines of python:
class Game:
def __init__(self) -> None:
self.token = 1
snakes_and_ladders_list = get_snakes_and_ladders()
self.sl = {}
for entry in snakes_and_ladders_list:
self.sl[entry[0]] = entry[1]
def move(self, howmany):
self.token += howmany
while (self.token in self.sl):
self.token = self.sl[self.token]
return self.token
def turn(self):
num = self.roll()
self.move(num)
if num == 6:
self.turn()
if self.token>=100:
return True
return False
def roll(self):
return randint(1,6)A turn consists of all the actions taken by a player before the next player gets their turn. This can consist of multiple moves if the player rolles one or more sixes, as rolling a six gives you another move.
With this, we can run some games and plot them. Here’s what a sample looks like.
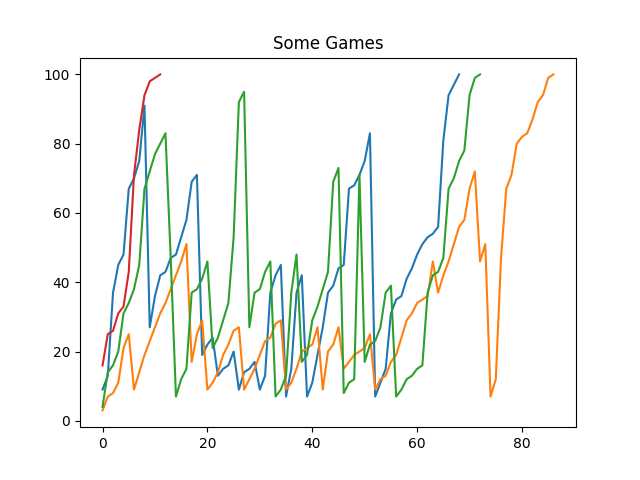
The Y axis is the position on the board, and the X axis is the number of turns. This small graphical representation of the game shows how variable it can be. The red player finishes in under 20 moves, whereas the orange player takes over 80.
To see how variable it is, we can run the simulation a large number of times and look at the results. Running for 10,000 games we get the following:
| function | result |
|---|---|
| min | 5 |
| max | 918 |
| mean | 90.32 |
| median | 65 |
So the fastest finish in 10,000 games was just 5 turns, and the slowest was an awful (if you were rolling the dice) 918 turns.
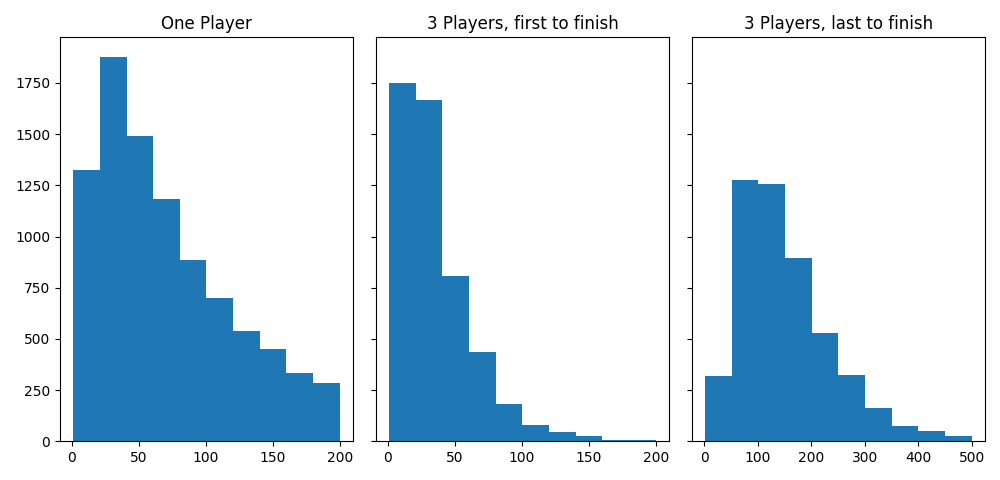
Here are some histograms for the distribution of game lengths, the distribution of number of turns for a player to win in a 3 person game, and the number of turns for all players to finish in a 3 person game.
The python code for this post is at snakes.py
